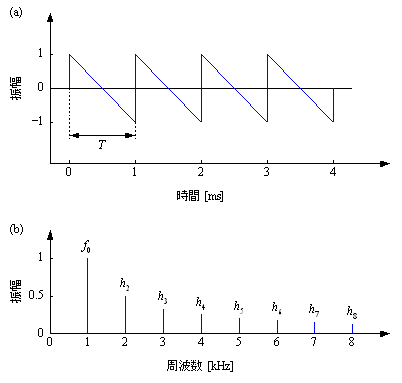
図1．ノコギリ波：(a) 波形, (b) 周波数特性
サウンドプログラミング1
科目名： メディアネットワーク実験IA（2022年～）
対象： メディアネットワークコース3年目
日時： 6月25日（火） - 26日（水）13:00～18:00
場所： M棟1階計算機室
レポート提出締切： 7月2日（火）13:00
レポート提出先： 情報エレクトロニクス棟6階6-08
連絡先： 青木 直史（Tel: 706-6532）（E-mail: aoki@ime.ist.hokudai.ac.jp）
目的
音はマルチメディアコンテンツを構成する重要な要素である．本実験は，Pythonによるプログラミングを通して，サウンド処理に対する理解を深めることを目的としている．
1．はじめに
本実験は，Jupyter Notebookを利用し，ブラウザを使ってプログラムを実行しながら進めるものとする．なお，音を確認する場合は各自のイヤフォンまたはヘッドフォンを使うこと．
(1) Jupyter Notebookの起動
Anaconda Promptを開く．
jupyter notebook
と入力して実行．
(2) ブラウザ（Chrome推奨）を利用してプログラミングを行う．
「New」ボタンをクリックして「Python3」を選択．
音ファイルや画像ファイルを利用するときは「Upload」ボタンをクリックし，必要なファイルをJupyter Notebookにアップロードすること．
サウンドプログラミングの前提として、以下の動画を参考に、各自、音響学について理解を深めること。
音響学講義「第1回 サイン波」
音響学講義「第2回 サイン波の重ね合わせ」
音響学講義「第3回 周波数分析」
音響学講義「第4回 音の性質」
音響学講義「第5回 音声」
サウンドプログラミング2（メディアネットワーク実験IIA）の手引書
サウンドプログラミング2
2．サイン波の音をつくる
どんなに複雑な音であっても大小さまざまなサイン波の重ね合わせによって合成できることが音響学の重要な原理になっている。これが、音響学のなかで最も基本となる音としてサイン波の音が位置づけられている理由になっている。（サイン波については、音響学講義「第1回 サイン波」、サイン波の重ね合わせについては、音響学講義「第2回 サイン波の重ね合わせ」を参考にしてください。）
以下のプログラムを実行しなさい．サイン波の音を耳で聞いて確かめなさい．
(1)
%matplotlib inline import numpy as np import matplotlib.pyplot as plt from scipy.io import wavfile from IPython.display import display, Audio
(2)
fs = 8000 duration = 1 length_of_s = int(fs * duration) s = np.zeros(length_of_s) for n in range(length_of_s): s[n] = 0.5 * np.sin(2 * np.pi * 1000 * n / fs)
(3)
for n in range(length_of_s): s[n] = (s[n] + 1) / 2 * 65536 s[n] = int(s[n] + 0.5) if s[n] > 65535: s[n] = 65535 elif s[n] < 0: s[n] = 0 s[n] -= 32768 wavfile.write('p1(output).wav', fs, s.astype(np.int16))
(4)
Audio('p1(output).wav')
3．音をながめる
以下のプログラムを実行しなさい．サイン波の音を目で見て確かめなさい．
(1)
%matplotlib inline import numpy as np import matplotlib.pyplot as plt from scipy.io import wavfile from IPython.display import display, Audio
(2)
def Hanning_window(N): w = np.zeros(N) if N % 2 == 0: for n in range(N): w[n] = 0.5 - 0.5 * np.cos(2 * np.pi * n / N) else: for n in range(N): w[n] = 0.5 - 0.5 * np.cos(2 * np.pi * (n + 0.5) / N) return w
(3)
fs, s = wavfile.read('p1(output).wav') s = s.astype(np.float) length_of_s = len(s) np.random.seed(0) for n in range(length_of_s): s[n] = s[n] + 32768 + (np.random.rand() - 0.5) s[n] = s[n] / 65536 * 2 - 1
(4)
t = np.zeros(length_of_s) for n in range(length_of_s): t[n] = n / fs
(5)
plt.figure() plt.plot(t, s) plt.axis([0, 0.008, -1, 1]) plt.xlabel("time [s]") plt.ylabel("amplitude") plt.savefig('waveform.png')
(6)
N = 1024 w = Hanning_window(N) x = np.zeros(N) for n in range(N): x[n] = s[n] * w[n]
(7)
X = np.fft.fft(x, N) X_abs = np.abs(X)
(8)
f = np.zeros(N) for k in range(N): f[k] = fs * k / N
(9)
plt.figure() plt.plot(f[0 : int(N / 2)], X_abs[0 : int(N / 2)]) plt.axis([0, 4000, 0, 200]) plt.xlabel("frequency [Hz]") plt.ylabel("amplitude") plt.savefig('frequency_characteristics.png')
4．スペクトログラム
スペクトログラムは，窓関数を少しずつずらしながら周波数分析を行い，横軸を時間，縦軸を周波数として，周波数特性を濃淡表示した2次元の画像である．（スペクトログラムについては、音響学講義「第3回 周波数分析」を参考にしてください。）
以下のプログラムを実行しなさい．サイン波の音のスペクトログラムを表示しなさい．
(1)
%matplotlib inline import numpy as np import matplotlib.pyplot as plt from scipy.io import wavfile from IPython.display import display, Audio
(2)
def Hanning_window(N): w = np.zeros(N) if N % 2 == 0: for n in range(N): w[n] = 0.5 - 0.5 * np.cos(2 * np.pi * n / N) else: for n in range(N): w[n] = 0.5 - 0.5 * np.cos(2 * np.pi * (n + 0.5) / N) return w
(3)
fs, s = wavfile.read('p1(output).wav') s = s.astype(np.float) length_of_s = len(s) np.random.seed(0) for n in range(length_of_s): s[n] = s[n] + 32768 + (np.random.rand() - 0.5) s[n] = s[n] / 65536 * 2 - 1
(4)
N = 512 shift_size = 64 number_of_frame = int((length_of_s - (N - shift_size)) / shift_size)
(5)
x = np.zeros(N) w = Hanning_window(N) S = np.zeros((int(N / 2 + 1), number_of_frame))
(6)
for frame in range(number_of_frame): offset = shift_size * frame for n in range(N): x[n] = s[offset + n] * w[n] X = np.fft.fft(x, N) X_abs = np.abs(X) for k in range(int(N / 2 + 1)): S[k, frame] = 20 * np.log10(X_abs[k])
(7)
plt.figure() xmin = (N / 2) / fs xmax = (shift_size * (number_of_frame - 1) + N / 2) / fs ymin = 0 ymax = fs / 2 plt.imshow(S, aspect = 'auto', cmap = 'Greys', origin = 'lower', vmin = 0, vmax = 20, extent = [xmin, xmax, ymin, ymax]) plt.axis([0, length_of_s / fs, 0, fs / 2]) plt.xlabel('time [s]') plt.ylabel('frequency [Hz]') plt.savefig('spectrogram.png')
課題
[1] 標本化周波数8kHzで、7kHzのサイン波を生成し、周波数特性のグラフを作成しなさい。サイン波の周波数はいくつになるか。その理由について考察しなさい。
[2] 標本化周波数8kHzで、9kHzのサイン波を生成し、周波数特性のグラフを作成しなさい。サイン波の周波数はいくつになるか。その理由について考察しなさい。
[3] 標本化周波数8kHzで、4kHzのサイン波を生成したところ、無音になった。こうした現象が発生した理由を述べよ。
[4] 図1に示すように、ノコギリ波は、i倍目の周波数の振幅が1/i倍になる波形として定義される。サイン波を無限に重ね合わせると、ノコギリ波の波形の1周期はつぎの式で近似できる。
s(t) = -2t/T + 1 (0 ≤ t < T)
図1．ノコギリ波：(a) 波形, (b) 周波数特性
この式の定義どおり、コンピュータを使ってつぎのようにノコギリ波を生成することは、はたして適切であるか考察せよ。
%matplotlib inline import numpy as np import matplotlib.pyplot as plt from scipy.io import wavfile from IPython.display import display, Audio fs = 8000 duration = 1 f0 = 600 T = fs / f0 length_of_s = int(fs * duration) s = np.zeros(length_of_s) x = 0 for n in range(length_of_s): s[n] = -2 * x + 1 delta = f0 / fs x += delta if x >= 1: x -= 1 for n in range(length_of_s): s[n] = (s[n] + 1) / 2 * 65536 s[n] = int(s[n] + 0.5) if s[n] > 65535: s[n] = 65535 elif s[n] < 0: s[n] = 0 s[n] -= 32768 wavfile.write('p4(output).wav', fs, s.astype(np.int16)) Audio('p4(output).wav')
5．分析合成
どんなに複雑な音であっても大小さまざまなサイン波の重ね合わせによって合成できることが音響学の重要な原理になっている。この原理を利用し、フーリエ変換によって音をサイン波の集合として表現したのち、サイン波の重ね合わせによって本来の音を再合成してみよう。
はじめに、スペクトログラムを求める。
(1)
%matplotlib inline import numpy as np import matplotlib.pyplot as plt from scipy.io import wavfile from IPython.display import display, Audio
(2)
def Hanning_window(N): w = np.zeros(N) if N % 2 == 0: for n in range(N): w[n] = 0.5 - 0.5 * np.cos(2 * np.pi * n / N) else: for n in range(N): w[n] = 0.5 - 0.5 * np.cos(2 * np.pi * (n + 0.5) / N) return w
(3)
fs, s = wavfile.read('vocal.wav') s = s.astype(np.float) length_of_s = len(s) np.random.seed(0) for n in range(length_of_s): s[n] = s[n] + 32768 + (np.random.rand() - 0.5) s[n] = s[n] / 65536 * 2 - 1
(4)
N = 4096 shift_size = int(N / 2) number_of_frame = int((length_of_s - (N - shift_size)) / shift_size)
(5)
x = np.zeros(N) w = Hanning_window(N) S_abs = np.zeros((int(N / 2 + 1), number_of_frame)) S_angle = np.zeros((int(N / 2 + 1), number_of_frame))
(6)
for frame in range(number_of_frame): offset = shift_size * frame for n in range(N): x[n] = s[offset + n] * w[n] X = np.fft.fft(x, N) X_abs = np.abs(X) X_angle = np.angle(X) for k in range(int(N / 2 + 1)): S_abs[k, frame] = X_abs[k] S_angle[k, frame] = X_angle[k]
(7)
plt.figure() xmin = (N / 2) / fs xmax = (shift_size * (number_of_frame - 1) + N / 2) / fs ymin = 0 ymax = fs / 2 plt.imshow(S_abs, aspect = 'auto', cmap = 'Greys', origin = 'lower', vmin = 0, vmax = 1, extent = [xmin, xmax, ymin, ymax]) plt.axis([0, length_of_s / fs, 0, fs / 2]) plt.xlabel('time [s]') plt.ylabel('frequency [Hz]') plt.savefig('spectrogram.png')
(8)
plt.figure() xmin = (N / 2) / fs xmax = (shift_size * (number_of_frame - 1) + N / 2) / fs ymin = 0 ymax = fs / 2 plt.imshow(S_angle, aspect = 'auto', cmap = 'Greys', origin = 'lower', vmin = -np.pi, vmax = np.pi, extent = [xmin, xmax, ymin, ymax]) plt.axis([0, length_of_s / fs, 0, fs / 2]) plt.xlabel('time [s]') plt.ylabel('frequency [Hz]') plt.savefig('spectrogram.png')
つづいて、スペクトログラムから、音声を再合成してみる。
(9)
Y_abs = np.zeros(N) Y_angle = np.zeros(N) s1 = np.zeros(length_of_s)
(10)
for frame in range(number_of_frame): offset = shift_size * frame for k in range(int(N / 2)): Y_abs[k] = S_abs[k, frame] Y_angle[k] = S_angle[k, frame] for k in range(1, int(N / 2)): Y_abs[N - k] = Y_abs[k] Y_angle[N - k] = -Y_angle[k] Y = Y_abs * np.exp(1j * Y_angle) y = np.fft.ifft(Y, N) y = np.real(y) for n in range(N): s1[offset + n] += y[n]
(11)
for n in range(length_of_s): s1[n] = (s1[n] + 1) / 2 * 65536 s1[n] = int(s1[n] + 0.5) if s1[n] > 65535: s1[n] = 65535 elif s1[n] < 0: s1[n] = 0 s1[n] -= 32768 wavfile.write('p6(output).wav', fs, s1.astype(np.int16))
(12)
Audio('p6(output).wav')
課題
[5] 通常、音声のスペクトログラムは、振幅スペクトルのみ表示し、位相スペクトルは表示しないことが一般的である。位相スペクトルを無視し、振幅スペクトルだけから音を再合成できるかどうか、実際にプログラムをつくって確認し、その結果について考察しなさい。
[6] スペクトログラムから振幅の大きい順番にサイン波を取り出し、重ね合わせることで、音を再合成するプログラムをつくりなさい。サイン波の数を少なくしていくと、どのように聞こえるか、また、少なくともいくつあれば、本来の音と同じように聞こえるか、比較して考察しなさい。スペクトログラムの差分を取ってみるなど、本来の音との違いを、数値によって表現する何らかの方法を使って、客観的に考察してみてください。
6．音声合成
図2と図3に示すように，特定の周波数成分が強調されているのが音声の特徴になっている．こうした帯域はフォルマントと呼ばれ，周波数の低いものから順番に，第1フォルマント（F1）、第2フォルマント（F2）、第3フォルマント（F3）、第4フォルマント（F4）と名前がつけられている．（音声については、音響学講義「第5回 音声」を参考にしてください。）
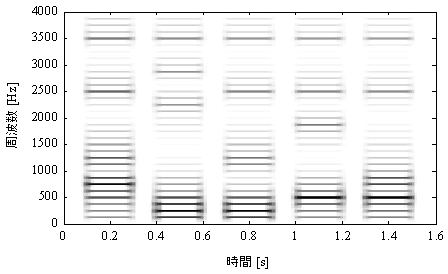
図2．音声の狭帯域スペクトログラム
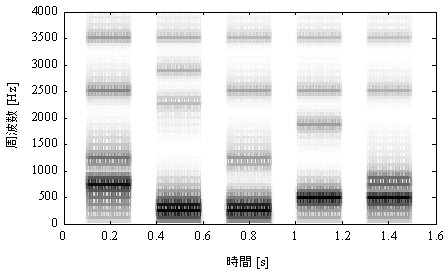
図3．音声の広帯域スペクトログラム
図4に示すように，それぞれのフォルマントをBPFとしてとらえると，音声の周波数エンベロープは複数のBPFを組み合わせたものとして解釈することができる．
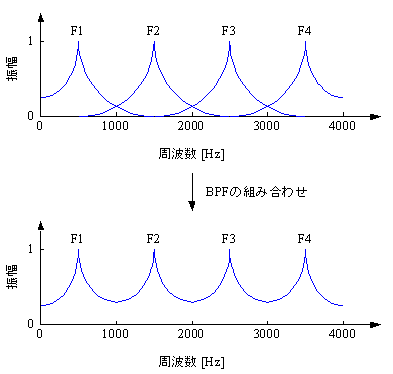
図4．音声の周波数エンベロープ
図5に示すように，フォルマントは音声によって異なる．こうした周波数エンベロープの特徴が音韻を識別するための重要な手がかりになっている．
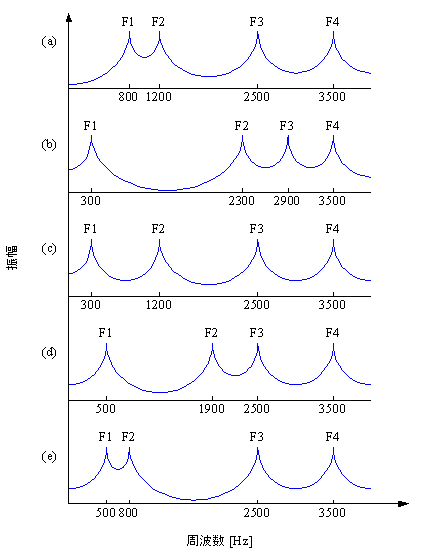
図5．音声の周波数エンベロープ：(a) ア, (b) イ, (c) ウ, (d) エ, (e) オ
声帯振動を音源、声道をフィルタとして、音声生成のしくみを説明しているのがソースフィルタ理論である。ここでは、ノコギリ波を原音、ふたつのBPFを声道フィルタとして、音声を合成してみることにする。
以下のプログラムを実行しなさい。
(1)
%matplotlib inline import numpy as np import matplotlib.pyplot as plt from scipy.io import wavfile from IPython.display import display, Audio
(2)
def BPF(fs, fc, Q): fc /= fs fc = np.tan(np.pi * fc) / (2 * np.pi) a = np.zeros(3) b = np.zeros(3) a[0] = 1 + 2 * np.pi * fc / Q + 4 * np.pi * np.pi * fc * fc a[1] = (8 * np.pi * np.pi * fc * fc - 2) / a[0] a[2] = (1 - 2 * np.pi * fc / Q + 4 * np.pi * np.pi * fc * fc) / a[0] b[0] = 2 * np.pi * fc / Q / a[0] b[1] = 0 b[2] = -2 * np.pi * fc / Q / a[0] a[0] = 1 return a, b
(3)
fs = 8000 duration = 1 f0 = 120 T = fs / f0 length_of_s = int(fs * duration) s0 = np.zeros(length_of_s)
(4)
x = 0 for n in range(length_of_s): s0[n] = - 2 * x + 1 delta = f0 / fs if 0 <= x and x < delta: t = x / delta d = -t * t + 2 * t - 1 s0[n] += d elif 1 - delta < x and x <= 1: t = (x - 1) / delta d = t * t + 2 * t + 1 s0[n] += d x += delta if x >= 1: x -= 1
(5)
s1 = np.zeros(length_of_s) fc = 800 Q = 800 / 100 a, b = BPF(fs, fc, Q) for n in range(length_of_s): for m in range(0, 3): if n - m >= 0: s1[n] += b[m] * s0[n - m] for m in range(1, 3): if n - m >= 0: s1[n] += -a[m] * s1[n - m] s2 = s1
(6)
s1 = np.zeros(length_of_s) fc = 1200 Q = 1200 / 100 a, b = BPF(fs, fc, Q) for n in range(length_of_s): for m in range(0, 3): if n - m >= 0: s1[n] += b[m] * s0[n - m] for m in range(1, 3): if n - m >= 0: s1[n] += -a[m] * s1[n - m] s2 += s1
(7)
for n in range(int(fs * 0.01)): s2[n] *= n / (fs * 0.01) s2[length_of_s - n - 1] *= n / (fs * 0.01) master_volume = 0.9 s2 /= np.max(np.abs(s2)) s2 *= master_volume
(8)
for n in range(length_of_s): s2[n] = (s2[n] + 1) / 2 * 65536 s2[n] = int(s2[n] + 0.5) if s2[n] > 65535: s2[n] = 65535 elif s2[n] < 0: s2[n] = 0 s2[n] -= 32768 wavfile.write('p7(output).wav', fs, s2.astype(np.int16))
(9)
Audio('p7(output).wav')
課題
[7] ウェブサイトなどから日本語の5母音の音データを入手し、周波数特性を調べることで、それぞれの母音ごとにBPFのfcやQがどのように分布しているか、分析の方法も含め、調査しなさい。なお、fcは中心周波数、Qはクオリティファクタであり、BPFの帯域幅をWとすると、Q=fc/Wの関係がある。
[8] 調査にもとづき、実際に日本語の5母音を合成しなさい。人間の音声と同じように聞こえるか、比較して考察しなさい。こうした合成音声を、人間の音声に似せるには、どのようなことに考慮する必要があるのか調査しなさい。 実際にプログラムをつくって確認してみてください。
（参考）フォルマントが時間的に変化することが連続音声の特徴であり、これを人間の聴覚は音韻の変化としてとらえている。Voice Pad（タブレット版）、または、Voice Pad（スマホ版）を使って、そのことを確認してみてください。
7．ボイスチェンジャ
ネットに動画を公開するためのツールとして、音声合成と並び、よく使われているのが、ボイスチェンジャである。
アナログ技術の時代から知られていることではあるが、録音した音の再生スピードを変化させると、性別が変化したように聞こえる。ボイスチェンジャとしてプリミティブな方法であるが、こうした処理は、ディジタル技術の場合、つぎのように，本来とは異なる標本化周波数で音データを再生することに等しい。
(1)
%matplotlib inline import numpy as np import matplotlib.pyplot as plt from scipy.io import wavfile from IPython.display import display, Audio
(2)
fs, s = wavfile.read('mono.wav') s = s.astype(np.float) length_of_s = len(s) np.random.seed(0) for n in range(length_of_s): s[n] = s[n] + 32768 + (np.random.rand() - 0.5) s[n] = s[n] / 65536 * 2 - 1
(3)
fs = 35280 # 44100 * 0.8
(4)
for n in range(length_of_s): s[n] = (s[n] + 1) / 2 * 65536 s[n] = int(s[n] + 0.5) if s[n] > 65535: s[n] = 65535 elif s[n] < 0: s[n] = 0 s[n] -= 32768 wavfile.write('p8(output).wav', fs, s.astype(np.int16))
(5)
Audio('p8(output).wav')
課題
[9] こうした処理によって、なぜ性別が変化したように聞こえるのか、声の高さとフォルマントというキーワードを含め、その理由について考察しなさい．
[10] フーリエ変換を使ったボイスチェンジャのしくみを考え、実際にプログラムをつくって確認してみてください。
参考文献
青木 直史, ``Pythonではじめる 音のプログラミング ～ コンピュータミュージックの信号処理 ～ ,'' オーム社, 2022.
青木 直史, ``ゼロからはじめる音響学,'' 講談社, 2014.
青木 直史, ``サウンドプログラミング入門 - 音響合成の基本とC言語による実装 - ,'' 技術評論社, 2013.
青木 直史, ``C言語ではじめる音のプログラミング - サウンドエフェクトの信号処理 - ,'' オーム社, 2008.
青木 直史, ``ディジタル・サウンド処理入門 - 音のプログラミングとMATLAB（Octave・Scilab）における実際 - ,'' CQ出版社, 2006.
Last Modified: July 1 12:00 JST 2023 by Naofumi Aoki
E-mail: aoki@ime.ist.hokudai.ac.jp